Skip to content

THIS IS A DRAFT

Implementation details/notes:

  • Methods:

    • Rings are generated with the cartopy.geodesic.Geodesic.circle method which solves the direct geodesic problem to generate a circle of equidistant points from a center point.
      • The reference ellipsoid is defined as:
        • [Params:]
          • Semimajor axis: 3395428 m
          • Flattening: 0.005227617843759314
        • [Citation:]
          • Ardalan, A. A., Karimi, R., & Grafarend, E. W. (2009). A New Reference Equipotential Surface, and Reference Ellipsoid for the Planet Mars. Earth, Moon, and Planets, 106, 1-13. https://doi.org/10.1007/s11038-009-9342-7

  • Reasoning:

    • Q: Why generate / average over multiple rings?
      • I don't think you can just generate a single geodesic circle at desired radius and interpolate lon/lat coordinates from the center to each point on the circle, since that's not the correct geodesic path!!!
      • My method of averaging over concentric rings is more complicated than the above but significantly more correct (i.e. geometrically perfect, I think). Not sure how much error is practically introduced by the prior method though.
    • Q: How do we determine the number of points per ring?
      • [Method 1, Fig 1 & Fig 2] Easy/straightforward method is for every ring to have a constant number of points (cartopy default is 180). The drawback is either inner rings have aggressively too many points or outer rings have too few points, which can get unnecessarily costly/annoying/inconsistent.
        • The example below took 0.878 seconds (just for data generation, not plotting) for 7,200 points.
      • [Method 2, Fig 3 & Fig 4] A more complex but efficient method is to make it so there's a constant distance between points on each ring (default is 5km). This way, we don't have to worry about tweaking the number of points per ring to eliminate inefficiency/inconsistency in the inner/outer rings -- i.e. run and forget about it.
        • The example below took 0.673 seconds for 4,933 points.

 

 

Figures

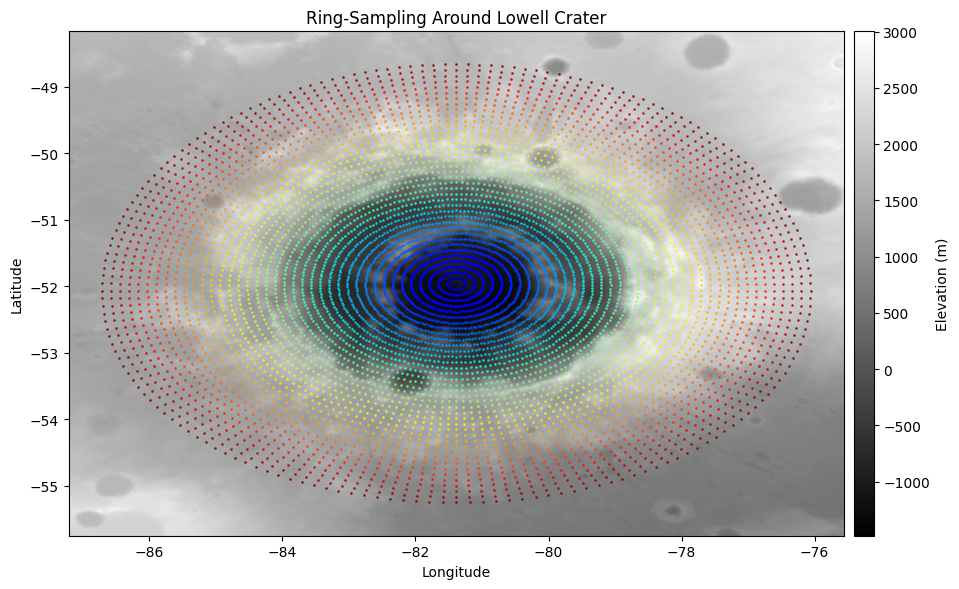
Figure 1: 180 points per ring.

 

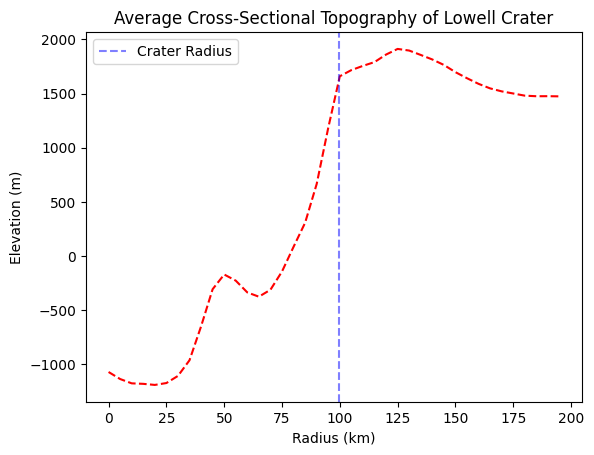
Figure 2: 180 points per ring.

 

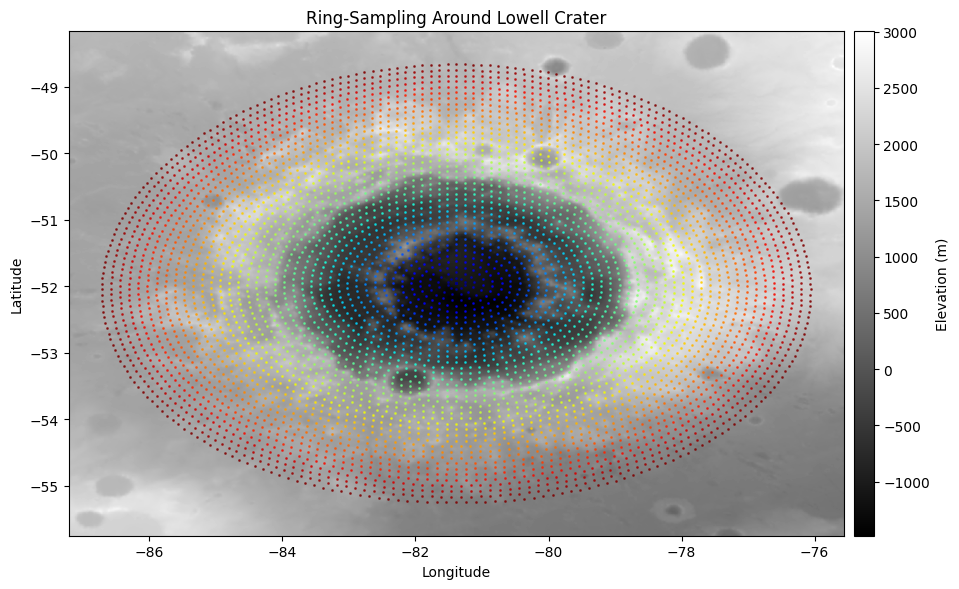
Figure 3: 5km between points on each ring.

 

Figure 4: 5km between points on each ring.